- Причины резонанса
- Принцип работы параллельного колебательного контура
- Характеристики резонанса
- Как найти резонанс параллельного колебательного контура на практике
- Резонанс токов и напряжений
- Собственная частота резонансного контура
- Электрический резонанс
- Добротность параллельного колебательного контура
- Применение параллельного колебательного контура
- Формула
- Формулировка
- Условия наступления
Причины резонанса
Классический пример с приказом командира идти марширующим солдатам «не в ногу» перед мостом наглядно демонстрирует суть этого явления. Если не использовать такую предосторожность, колебания могут увеличиться до критичного значения, вплоть до разрушения конструкции. Для получения максимальной амплитуды раскачивают в определенном ритме качели. Приведенные примеры демонстрируют существенное увеличение результата при совпадении частот внешнего воздействия и непосредственно самой системы.
Электрический резонанс по своим принципам не отличается от механических аналогов. Он образуется при совпадении частот внешнего сигнала и контура. Функции накопителей энергии выполняют реактивные индукционные и емкостные элементы. Потери (постепенное уменьшение амплитуды) обеспечивает электрическое сопротивление цепи, что аналогично коэффициенту трения.
Принцип работы параллельного колебательного контура
Для создания необходимых условий электро резонанса необходимо создать параллельный контур с тремя типовыми компонентами:
- сопротивлением (R);
- емкостью (C);
- индуктивностью (L).
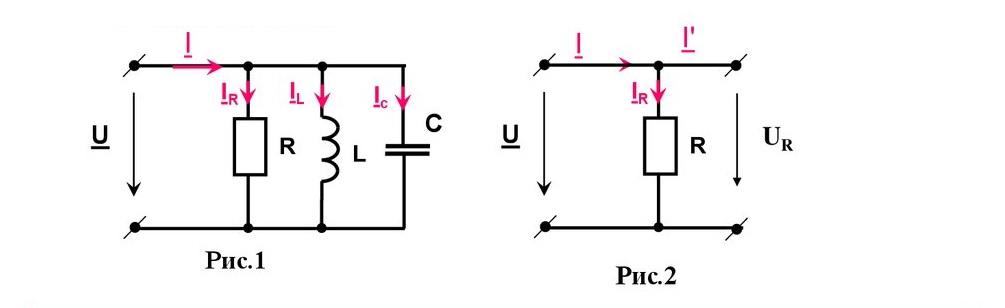
Схему подключают к источнику питания с напряжением (U)
На определенной частоте суммарные стоки через реактивные элементы (IL, Ic) становятся значительно больше, чем ток источника (I). Это явление называют резонансом тока.
Давайте подцепим к генератору частоты реальный параллельный колебательный контур
Что будет, если мы подадим на контур ток с частотой в ноль Герц, то есть постоянный ток? Он спокойно побежит через катушку и будет ограничиваться лишь сопротивлением потерь R самой катушки. Через конденсатор ток не побежит, потому что конденсатор не пропускает постоянный ток. Об это я писал еще в статье конденсатор в цепи постоянного и переменного тока.
Давайте тогда будем добавлять частоту. Итак, с увеличением частоты у нас конденсатор и катушка начнут оказывать реактивное сопротивление электрическому току.
Реактивное сопротивление катушки выражается по формуле
а конденсатора по формуле
Более подробно про это можно прочитать в этой статье.
Если плавно увеличивать частоту, то можно понять из формул, что в самом начале при плавном увеличении частоты конденсатор будет оказывать бОльшее сопротивление, чем катушка индуктивности. На какой-то частоте реактивные сопротивления катушки XL и конденсатора XC уравняются. Если далее увеличивать частоту, то уже катушка уже будет оказывать большее сопротивление, чем конденсатор.
Характеристики резонанса
Это явление образуется при одинаковых реактивных составляющих цепи. Такое распределение позволяет обеспечить равномерную циркуляцию магнитной и электрической составляющих энергии (через индуктивность и конденсатор, соответственно). Такой контур называют «колебательным» по аналогии с механическим маятником.
При достижении определенной резонансной частоты (w) в параллельном (последовательном) контуре импеданс максимален (минимален). Соответствующим образом при изменении электрического сопротивления уменьшается (увеличивается) ток.
Как найти резонанс параллельного колебательного контура на практике
Классическим примером применения резонанса колебательных контуров является настройка радиоприёмника на частоту соответствующей радиостанции. В качестве рабочего элемента настроечного узла используется конденсатор с регулируемой ёмкостью. Вращение ручки настройки изменяет ёмкость конденсатора, а значит и резонансную частоту контура.
В момент совпадения резонансной частоты с рабочей частотой какой-либо радиостанции возникает резонанс напряжений, в результате которого резко возрастает амплитуда колебаний принятой радиоприёмником частоты. Специальные фильтры отделяют эти колебания от несущих радиочастот, а усилители усиливают полученные сигналы. В динамике появляются звуки, генерируемые передатчиком радиостанции.

Колебательные контуры, построенные на принципе последовательного соединения LC-элементов, применяются в цепях питания высокоомных нагрузок, потребляющих токи повышенного напряжения. Такие же устройства применяют в полосовых фильтрах.
Последовательный резонанс применяют при пониженных напряжениях сети. В этом случае используют реактивную энергию обмоток трансформатора, соединённых последовательно.
Конденсаторы и различные катушки индуктивности (рис. 5) входят в конструкцию практически всех аналоговых устройств. Они используются для настройки фильтров или для управления токами в отдельных узлах.

Важно знать, что резонансные контуры не увеличивают количество электрической энергии в цепях. Они лишь могут повышать напряжения, иногда до опасных значений. Постоянный ток не причиной резонансных явлений.
Ладно, ближе к делу. Берем паяльник в руки и спаиваем катушку и конденсатор параллельно. Катушка на 22 мкГн, а конденсатор на 1000пФ.
На генераторе мы будет менять частоту, а с клемм X1 и X2 мы будем снимать напряжение и смотреть его на осциллографе.
Нетрудно догадаться, что у нас сопротивление параллельного колебательного контура будет зависеть от частоты генератора, так как в этом колебательном контуре мы видим два радиоэлемента, чьи реактивные сопротивления напрямую зависит от частоты, поэтому заменим колебательный контур эквивалентным сопротивлением контура Rкон.

Интересно, на что похожа эта схема? Не на делитель ли напряжения? Именно! Итак, вспоминаем правило делителя напряжения: на меньшем сопротивлении падает меньшее напряжение, на бОльшем сопротивлении падает бОльшее напряжение. Какой вывод можно сделать применительно к нашему колебательному контуру? Да все просто: на резонансной частоте сопротивление Rкон будет максимальным, вследствие чего у нас на этом сопротивлении “упадет” бОльшее напряжение.
Начинаем наш опыт. Поднимаем частоту на генераторе, начиная с самых маленьких частот.
200 Герц.
Как вы видите, на колебательном контуре “падает” малое напряжение, значит, по правилу делителя напряжения, можно сказать, что сейчас у контура малое сопротивление Rкон
Добавляем частоту. 11,4 Килогерца
Как вы видите, напряжение на контуре поднялось. Это значит, что сопротивление колебательного контура увеличилось.
Добавляем еще частоту. 50 Килогерц
Заметьте, напряжение на контуре повысилось еще больше. Значит его сопротивление еще больше увеличилось.
723 Килогерца
Обратите внимание на цену деления одного квадратика по вертикали, по сравнению с прошлым опытом. Там было 20мВ на один квадратик, а сейчас уже 500 мВ на один квадратик. Напряжение выросло, так как сопротивление колебательного контура стало еще больше.
И вот я поймал такую частоту, на которой получилось максимальное напряжение на колебательном контуре. Обратите внимание на цену деления по вертикали. Она равняется двум Вольтам.
Резонанс токов и напряжений
Параллельный контур используют, чтобы создать резонанс тока. Для выполнения отмеченных выше условий выбирают равные значения реактивных проводимостей (BL и Bc). По мере увеличения частоты общее сопротивление контура возрастает, что сопровождается уменьшением силы тока.
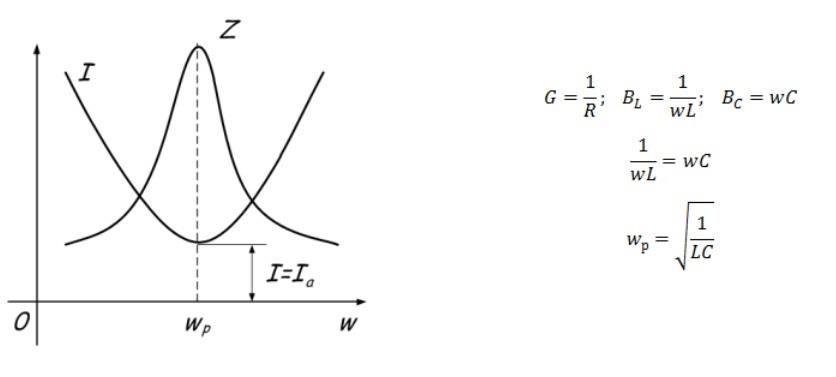
График изменения тока и проводимости, формулы для расчетов
В последовательном резонансном контуре устанавливают аналогичные функциональные компоненты. Эта схема при достижении резонансной частоты уменьшает сопротивление, что сопровождается существенным увеличением напряжения на реактивных составляющих, по сравнению с электродвижущей силой источника питания.
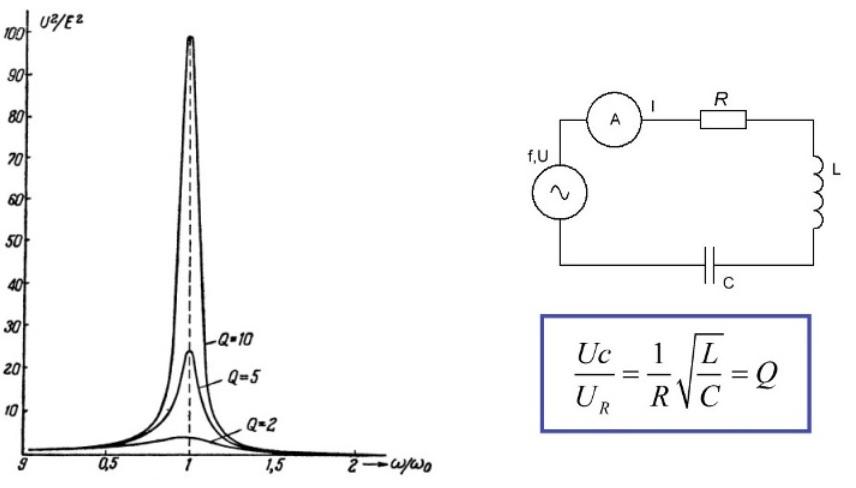
Резонанс напряжений в цепи переменного тока: график, электрическая схема и формула расчета
Применение последовательного колебательного контура удобно изучать на конкретном примере. При конструировании передающих устройств, например, уменьшение импеданса на определенной частоте позволяет сделать настройку на определенный сигнал. Такую задачу решают с помощью колебательного контура.
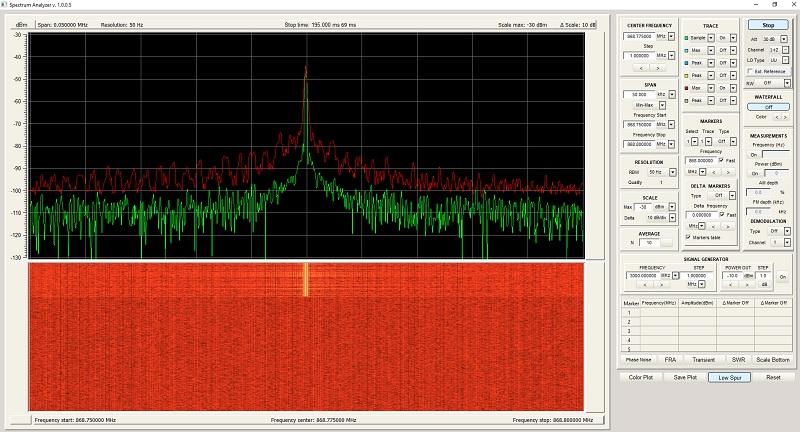
Распределение спектра на экране измерительного прибора после обработки фильтром
Точно спроектированный фильтр будет «убирать» паразитные составляющие без дополнительных средств контроля и автоматизации. Такое решение, кроме простоты и минимальной стоимости, обеспечивает экономное потребление энергии генератором сигнала.
Как показано на практических примерах, резонанс может выполнять полезные и вредные функции. Точный расчет поможет создать качественную электрическую цепь с заданными техническими параметрами.
Собственная частота резонансного контура
w = 1/√ L*C.
Если частота контура совпадает с частотой внешнего сигнала, амплитуда колебаний значительно увеличивается.
Резонанс в электрических цепях используют для фильтрации сигналов. Выбирают соответствующую схему обработки для ограничения необходимого диапазона либо расширения полосы пропускания.
С помощью последовательного контура можно повысить напряжение питания, если снабжающая организация не обеспечивает стабильность параметров сети. Такие неприятности встречаются при подключении потребителей на дачных участках и в коттеджных поселках, в сравнительно небольших населенных пунктах.
Недостаток ликвидируют конденсаторами, которые добавляют в электрическую цепь. Подобные решения помогают восстановить работоспособность дрели, станка, другого мощного оборудования. Обмотки соответствующего привода выполняют функции индуктивного компонента колебательного контура.
Параллельное подключение конденсаторов компенсирует потери, созданные реактивной мощностью. Этот вариант обеспечивает циркуляцию энергии между накопителем и подключенной обмоткой. Без такого дополнения часть энергии будет бесполезно потребляться сетью питания. Следует подчеркнуть, что счетчик в любом случае фиксирует потребление. Данная модернизация поможет сэкономить на оплате коммунальных услуг.
Резонансные явления способны чрезмерно увеличить силу тока или напряжение. Необходим точный расчет электрических цепей, чтобы предотвратить перегрев и повреждение проводов, короткие замыкания и другие аварийные ситуации.
Давайте более подробно рассмотрим эту осциллограмму, когда у нас было максимальное напряжение с контура.
Что здесь у нас произошло?
Электрический резонанс
Z = √ R2 (2π * f * L – 1/2π * f * C)2.
I = U/Z = U/ √ R2 (2π * f * L – 1/2π * f * C)2.
Если соблюдается равенство реактивных составляющих, сопротивление уменьшается с одновременным увеличением силы тока. При соблюдении такого условия несложно вычислить резонансную частоту (Fрез):
- 2π * f * L = 1/2π * f * C;
- Fрез = 1/2π * √ L*C.
Получить наибольшую амплитуду в последовательном контуре можно с помощью изменения следующих параметров:
- индуктивности;
- емкости;
- частоты.
C = 1/ f2 * L.
Если реактивные компоненты значительно больше активного сопротивления, на клеммах конденсатора или катушки можно получить повышение напряжения, по сравнению с источником.
В параллельном контуре оперируют с понятиями реактивных проводимостей (BL и Bc). Как и в предыдущем примере, для создания резонансного режима необходимо обеспечить равенство этих параметров. Дополнительным условием является совпадение частот (источника и контура). Ток при резонансе будет проходить только через активное сопротивление R.
Добротность параллельного колебательного контура
Кстати, этот контурный ток будет намного больше, чем ток, который проходит через контур. И знаете во сколько раз? Правильно, в Q раз. Q – это и есть добротность! В параллельном колебательном контуре она показывает во сколько раз сила тока в контуре Iкон больше сила тока в общей цепи Iрез

Q – добротность
R – сопротивление потерь на катушке, Ом
С – емкость, Ф
L – индуктивность, Гн
Применение параллельного колебательного контура
Если в некой электрической цепи (см. рис. 1) имеются ёмкостные и индуктивные элементы, которые обладают собственными резонансными частотами, то при совпадении этих частот амплитуда колебаний резко возрастёт. То есть происходит резкий всплеск напряжений на этих элементах. Это может вызвать разрушение элементов электрической цепи.

Давайте рассмотрим на этом примере, какие явления будут происходить при подключении генератора переменного тока к контактам схемы. Заметим, что катушки и конденсаторы обладают свойствами, которые можно сравнить с аналогом реактивного резистора. В частности, дроссель в электрической цепи создаёт индуктивное сопротивление. Конденсатор является причиной ёмкостного сопротивления.
Индуктивный элемент вызывает сдвиг фаз, характеризующийся отставанием тока от напряжения на ¼ периода. Под действием конденсатора ток, наоборот, на ¼ периода опережает напряжение.
Другими словами, действие индуктивности противоположно действию на сдвиг фаз ёмкостного сопротивления. То есть катушки индуктивности и ёмкостные элементы по-разному воздействуют на генератор и по-своему корректируют фазовые соотношения между электрическим током и напряжением.
Формула
Общее реактивное сопротивление рассматриваемых нами элементов равно сумме сопротивлений каждого из них. С учётом противоположности действий можно записать: Xобщ = XL — Xc , где XL = ωL — индуктивное реактивное сопротивление, выражение Xc = 1/ωC — это ёмкостное реактивное сопротивление.
На рисунке 2 изображены графики зависимости полного сопротивления цепи и связанной с ним силы тока, от реактивного сопротивления индуктивного элемента. Обратите внимание на то, как падает полное сопротивление при уменьшении реактивной сопротивляемости RL (график б) и как при этом возрастает ток (график в).

Электрические цепи, состоящие из последовательно соединённых конденсаторов, пассивный резисторов и катушек индуктивности называют последовательными резонансными (колебательными) контурами (см. рис. 2). Существуют также параллельные контуры, в которых R, L, C элементы подключены параллельно (рис. 3).

K = Uвых / Uвх = UC0 / U = Q
Формулировка
Описанное явление довольно распространено в электротехнике. Иногда с ним борются, а иногда специально создают условия для образования резонанса. Основными характеристиками всякого резонансного контура являются параметры добротности и частоты [ 1 ].
где R – общее активное сопротивление.
Учитывая, что по закону Ома U = I/Z, можно утверждать, что общее напряжение в цепи зависит, в том числе, и от слагаемых индуктивного и ёмкостного сопротивлений.
Если бы в рассматриваемой схеме (рис. 1) отсутствовало активное сопротивление R, то значение полного сопротивления Z стремилось бы к 0. Следовательно, напряжение на реактивных элементах при этом возрастает до критического уровня.
Поскольку XL и Xc зависят от частоты входного напряжения, то для возникновения резонанса следует подобрать соответствующую частоту сети, или изменять параметры катушки, либо конденсатора до тех пор, пока резонансные частоты не совпадут. Любое нарушение условий резонанса немедленно приводит к выходу системы из резонансного режима с последующим падением напряжения.
Условия наступления

Резонансные явления наступают только при наличии следующих условий:
- Наличие минимального активного сопротивления на участке электрической цепи.
- Равенство реактивных сопротивлений, возникших на цепочке LC.
- Совпадение входной частоты источника питания с резонансной частотой колебательного контура.
При резонансе в контуре напряжения на его элементах могут повышаться на порядок и больше.
Параллельный колебательный контур применяется в радиоприемном оборудовании, где надо выделить частоту какой-либо станции. Также с помощью колебательного контура можно построить различные резонансные фильтры.
w = 1/√ L*C.






