- Площадь равнобедренного треугольника через боковые стороны и угол между ними
- Площадь треугольника через две стороны и угол между ними
- Площадь треугольника через основание и высоту
- Площадь треугольника через радиус описанной окружности и 3 стороны
- Площадь треугольника через радиус вписанной окружности и 3 стороны
- Площадь треугольника через сторону и два прилежащих угла
- Площадь треугольника по формуле Герона
- Площадь прямоугольного треугольника через 2 стороны
- Площадь прямоугольного треугольника через гипотенузу и острый угол
- Площадь прямоугольного треугольника через катет и прилежащий угол
- Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
- Площадь прямоугольного треугольника через вписанную окружность
- Площадь прямоугольного треугольника по формуле Герона
- Площадь равнобедренного треугольника через основание и сторону
- Площадь равнобедренного треугольника через основание и угол
- Площадь равнобедренного треугольника через основание и высоту
- Площадь равнобедренного треугольника через боковые стороны и угол между ними
- Площадь равнобедренного треугольника через основание и угол между боковыми сторонами
- Площадь равностороннего треугольника через радиус описанной окружности
- Площадь равностороннего треугольника через радиус вписанной окружности
- Площадь равностороннего треугольника через сторону
- Площадь равностороннего треугольника через высоту
- Третий вариант решения задачи
Площадь равнобедренного треугольника через боковые стороны и угол между ними
Площадь треугольника через две стороны и угол между ними
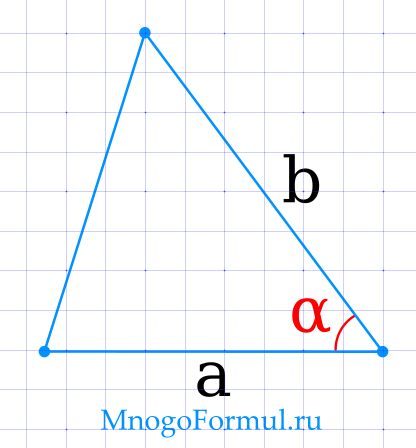
{S= dfrac{1}{2} cdot a cdot b cdot sin (alpha)}
{S= dfrac{1}{2} cdot a cdot b cdot sin (alpha)}, где a, b — стороны треугольника, α — угол между ними.
Площадь треугольника через основание и высоту
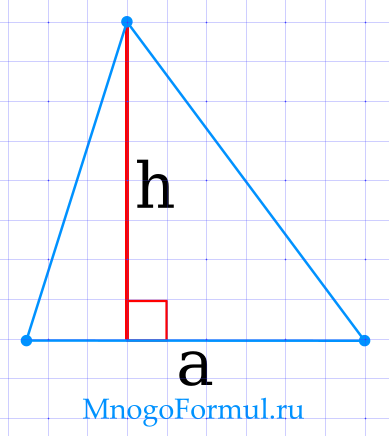
{S= dfrac{1}{2} cdot a cdot h}
{S= dfrac{1}{2} cdot a cdot h}, где a — основание треугольника, h — высота треугольника.
Площадь треугольника через радиус описанной окружности и 3 стороны
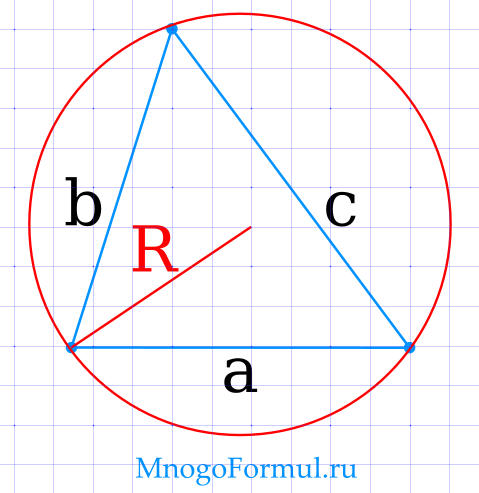
{S= dfrac{a cdot b cdot c}{4 cdot R}}
https://www.youtube.com/watch?v=upload
{S= dfrac{a cdot b cdot c}{4 cdot R}}, где a, b, c — стороны треугольника, R — радиус описанной окружности.
Площадь треугольника через радиус вписанной окружности и 3 стороны
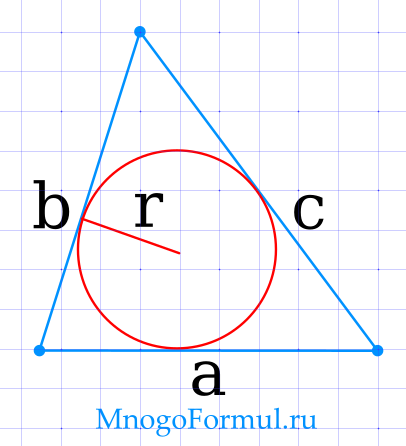
{S= r cdot dfrac{a b c}{2}}
{S= r cdot dfrac{a b c}{2}}, где a, b, c — стороны треугольника, r — радиус вписанной окружности.
Формулу можно переписать иначе, если учитывать, что {dfrac{a b c}{2}} — полупериметр треугольника. В этом случае формула будет выглядеть так: S = {r cdot p}, где p — полупериметр треугольника.
Площадь треугольника через сторону и два прилежащих угла
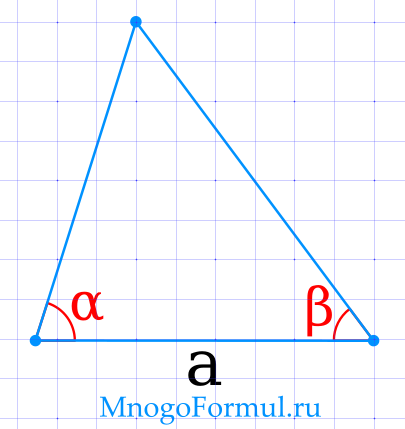
{S= dfrac{a^2}{2} cdot dfrac{sin(alpha) cdot sin(beta)}{sin(gamma)}}
{gamma = 180 — (alpha beta)}
{gamma = 180 — (alpha beta)}
Площадь треугольника по формуле Герона
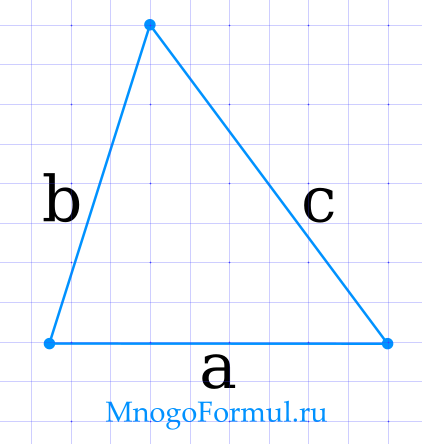
{S= sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a b c}{2}}
{S= sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}, где a, b, c — стороны треугольника, p — полупериметр треугольника, который можно найти по формуле p = {dfrac{a b c}{2}}

{S= dfrac{1}{2} cdot a cdot b cdot sin (alpha)}

{S= dfrac{1}{2} cdot a cdot h}

{S= dfrac{a cdot b cdot c}{4 cdot R}}

{S= r cdot dfrac{a b c}{2}}

{S= dfrac{a^2}{2} cdot dfrac{sin(alpha) cdot sin(beta)}{sin(gamma)}}
{gamma = 180 — (alpha beta)}

{S= sqrt{p cdot (p-a) cdot (p-b) cdot (p-c)}}
{p= dfrac{a b c}{2}}
Площадь прямоугольного треугольника через 2 стороны
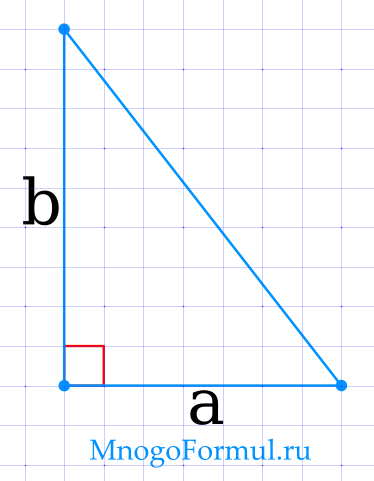
{S= dfrac{1}{2} cdot a cdot b}
{S= dfrac{1}{2} cdot a cdot b}, где a, b — стороны треугольника.
Площадь прямоугольного треугольника через гипотенузу и острый угол
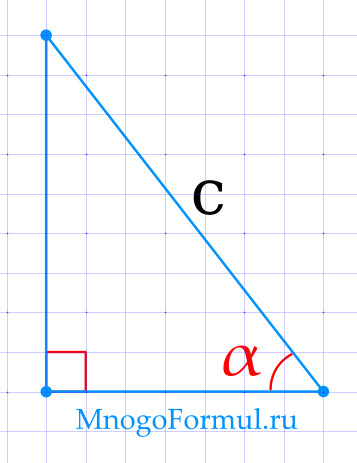
{S= dfrac{1}{4} cdot c^2 cdot sin (2 alpha)}
{S= dfrac{1}{4} cdot c^2 cdot sin (2 alpha)}, где c — гипотенуза треугольника, α — любой из прилегающих острых углов.
Площадь прямоугольного треугольника через катет и прилежащий угол
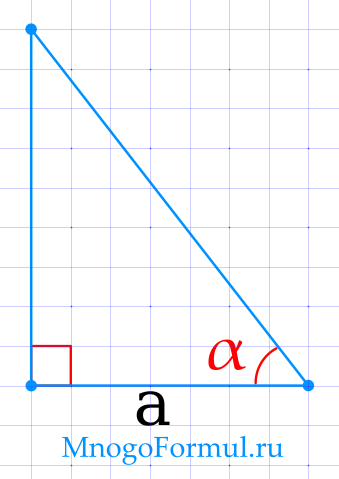
{S= dfrac{1}{2} cdot a^2 cdot tg (alpha)}

{S= dfrac{1}{2} cdot a^2 cdot tg (alpha)}, где a — катет треугольника, α — прилежащий угол.
Площадь прямоугольного треугольника через радиус вписанной окружности и гипотенузу
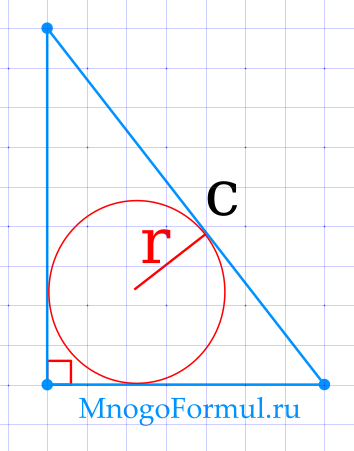
{S= r cdot (r c)}
{S= r cdot (r c)}, где c — гипотенуза треугольника, r — радиус вписанной окружности.
Площадь прямоугольного треугольника через вписанную окружность
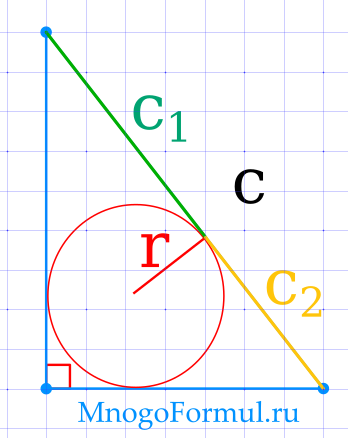
{S= c_{1} cdot c_{2}}
{S= c_{1} cdot c_{2}}, где c1 и c2 — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
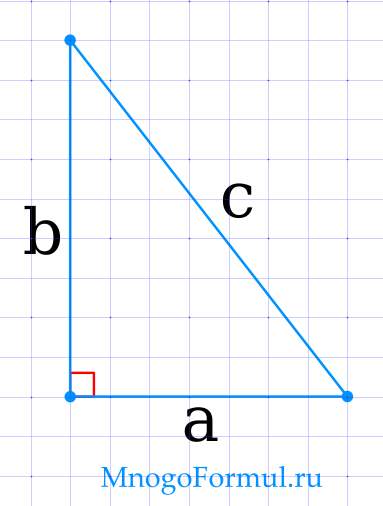
{S= (p-a) cdot (p-b)}
{p= dfrac{a b c}{2}}
{S= (p-a) cdot (p-b)}, где a, b — катеты треугольника, p — полупериметр прямоугольного треугольника, который рассчитывается по формуле p = {dfrac{a b c}{2}}

{S= dfrac{1}{2} cdot a cdot b}

{S= dfrac{1}{4} cdot c^2 cdot sin (2 alpha)}

{S= dfrac{1}{2} cdot a^2 cdot tg (alpha)}

{S= r cdot (r c)}

{S= c_{1} cdot c_{2}}

{S= (p-a) cdot (p-b)}
{p= dfrac{a b c}{2}}
Площадь равнобедренного треугольника через основание и сторону
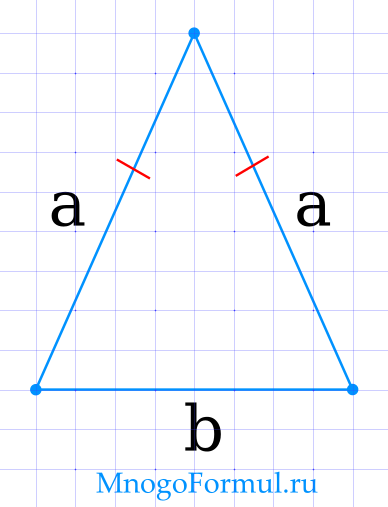
{S=dfrac{b}{4} sqrt{4 cdot a^2-b^2}}
{S=dfrac{b}{4} sqrt{4 cdot a^2-b^2}}, где a — боковая сторона треугольника, b — основание треугольника
Площадь равнобедренного треугольника через основание и угол
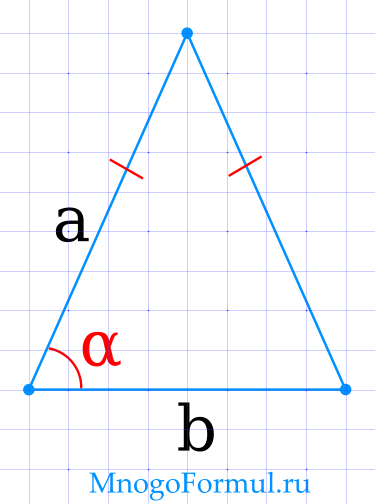
{S=dfrac{1}{2} cdot a cdot b cdot sin( alpha)}
https://www.youtube.com/watch?v=https:jCtM27FFZ9I
{S=dfrac{1}{2} cdot a cdot b cdot sin( alpha)}, где a — боковая сторона треугольника, b — основание треугольника, α — угол между основанием и стороной.
Площадь равнобедренного треугольника через основание и высоту
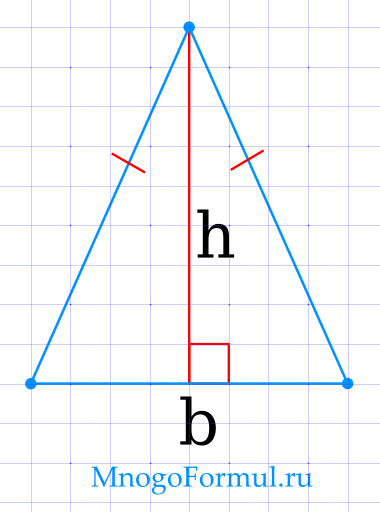
{S=dfrac{1}{2} cdot b cdot h}
{S=dfrac{1}{2} cdot b cdot h}, где b — основание треугольника, h — высота, проведенная к основанию.
Площадь равнобедренного треугольника через боковые стороны и угол между ними
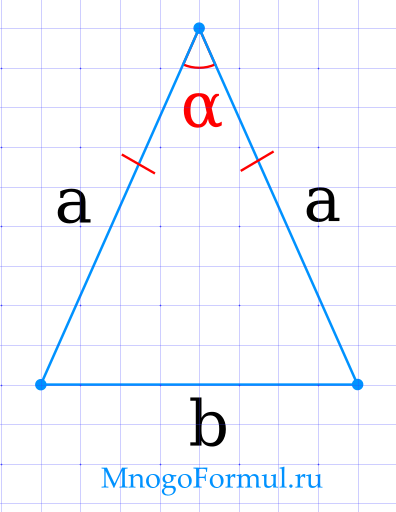
{S=dfrac{1}{2} cdot a^2 cdot sin(alpha)}

{S=dfrac{1}{2} cdot a^2 cdot sin(alpha)}, где a — боковая сторона треугольника, α — угол между боковыми сторонами.
Площадь равнобедренного треугольника через основание и угол между боковыми сторонами
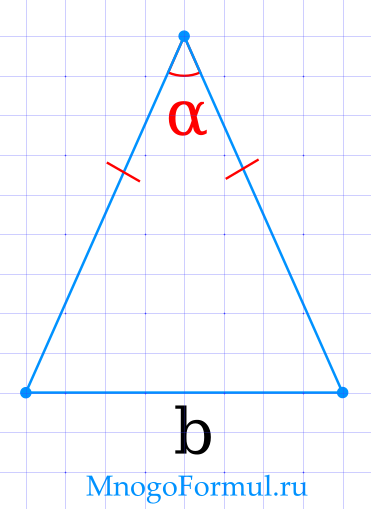
{S=dfrac{b^2}{4 cdot tg dfrac{alpha}{2}}}
{S=dfrac{b^2}{4 cdot tg dfrac{alpha}{2}}}, где b — основание треугольника, α — угол между боковыми сторонами.

{S=dfrac{b}{4} sqrt{4 cdot a^2-b^2}}

{S=dfrac{1}{2} cdot a cdot b cdot sin( alpha)}

{S=dfrac{1}{2} cdot b cdot h}

{S=dfrac{1}{2} cdot a^2 cdot sin(alpha)}

{S=dfrac{b^2}{4 cdot tg dfrac{alpha}{2}}}
Площадь равностороннего треугольника через радиус описанной окружности
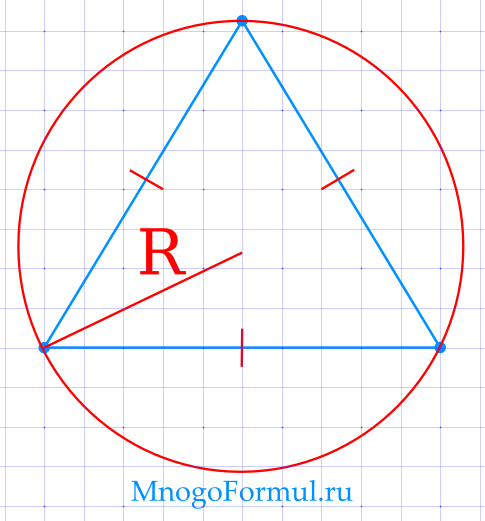
{S= dfrac{3 sqrt{3} cdot R^2}{4}}
{S= dfrac{3 sqrt{3} cdot R^2}{4}}, где R — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
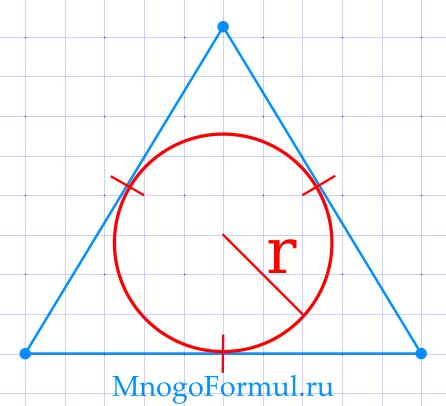
{S= 3 sqrt{3} cdot r^2}
{S= 3 sqrt{3} cdot r^2}, где r — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
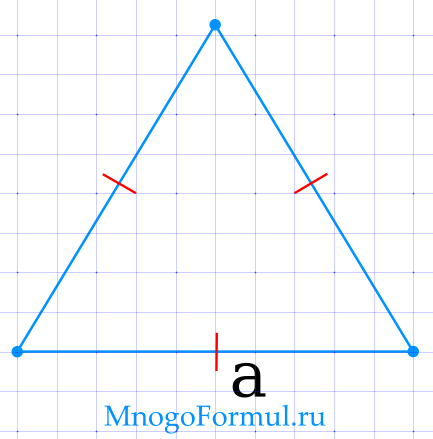
{S= dfrac{sqrt{3} cdot a^2}{4}}
{S= dfrac{sqrt{3} cdot a^2}{4}}, где a — сторона треугольника.
Площадь равностороннего треугольника через высоту
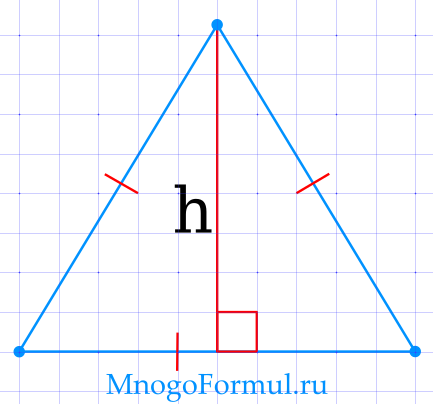
{S= dfrac{h^2}{sqrt{3}}}
{S= dfrac{h^2}{sqrt{3}}}, где h — высота треугольника.
Просмотров страницы: 174800

{S= dfrac{3 sqrt{3} cdot R^2}{4}}

{S= 3 sqrt{3} cdot r^2}

{S= dfrac{sqrt{3} cdot a^2}{4}}

{S= dfrac{h^2}{sqrt{3}}}
Третий вариант решения задачи
p – полупериметр треугольника.
На вход программе подаются целые числа, выводом программы должно являться вещественное число, соответствующее площади треугольника.
Для ввода целых чисел используем функцию int().
import math
Код программы для вычисления площади треугольника
import math #подключаем библиотеку математических функций
a=int(input("Введите сторону a="))
b=int(input(Введите сторону b=))
c=int(input(Введите сторону c=))
p=(a b c)/2
s=math.sqrt(p*(p-a)*(p-b)*(p-c))
print(s)
https://www.youtube.com/watch?v=https:cn_YJ0LVuyU
Результат выполнения кода программы
Python 3.5.2 (default, Dec 2015, 13:05:11)
[GCC 4.8.2] on Linux
12
13
14
72.30793524918272
Также можно воспользоваться стандартной функцией возведения числа в степень. Дело в том, что квадратный корень — это возведение в степень 1/2.
где x — число, возводимое в степень, а y — сама степень.
s=pow((p*(p-a)*(p-b)*(p-c)),1/2)
https://www.youtube.com/watch?v=https:tv.youtube.com
Вместо извлечения корня можно возвести в степень 1/2 или 0,5. При этому функцию использовать не нужно.
s=(p*(p-a)*(p-b)*(p-c))**0.5
Как видим, результат выполнения программы точно такой же.
Нахождение натуральных чисел с условием Вычисление площади фигур